Snappy Animations

Numerical Tricks for Low-Latency Visual Feedback

Automaticity: acting without thinking

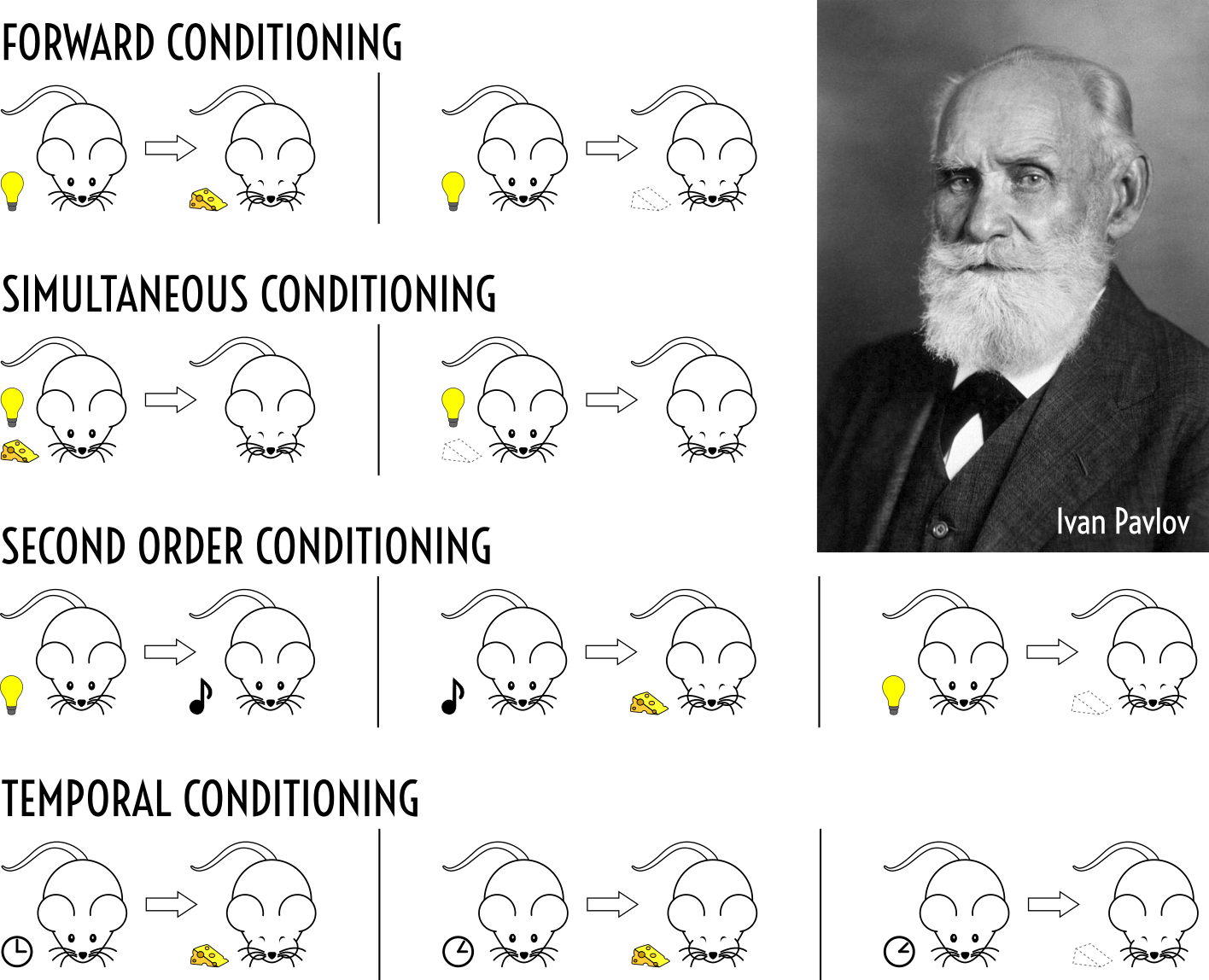
Classical conditioning can produce automaticity.

Not the kind of automaticity that we're interested in.

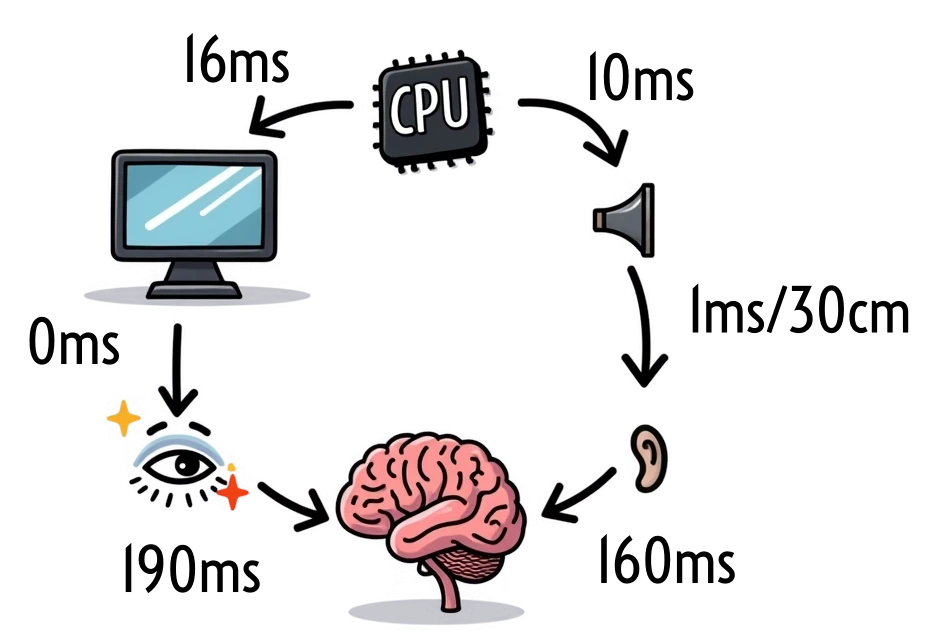
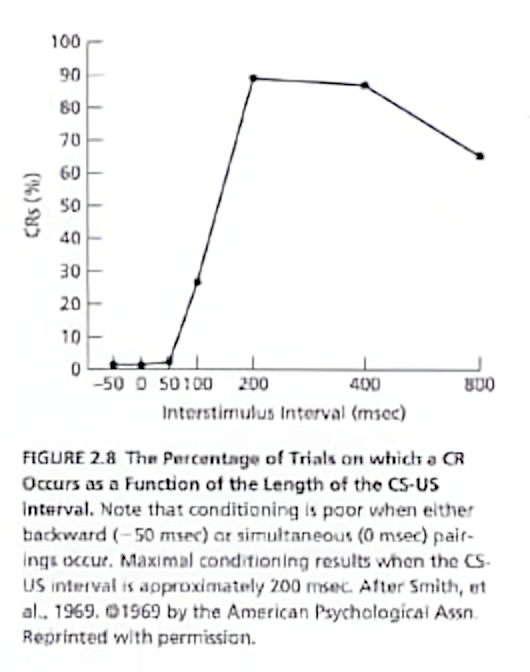
Classical conditioning requires some latency ≠ 0.

Understanding / mental model of the task is optional.

Obtaining Automaticity:

• repetition
• reinforcement
• immersion

Known problem → New domain

User interface

Agenda

1. Intro to user interfaces & latency
2. Pros & cons of animation techniques
3. Formulas for animated approach
4. Drag & drop
5. Final tips

Timeline-based animation

Simulation-driven animation

Springy attachment

Synchronization

Power draw

Timeline vs Procedural

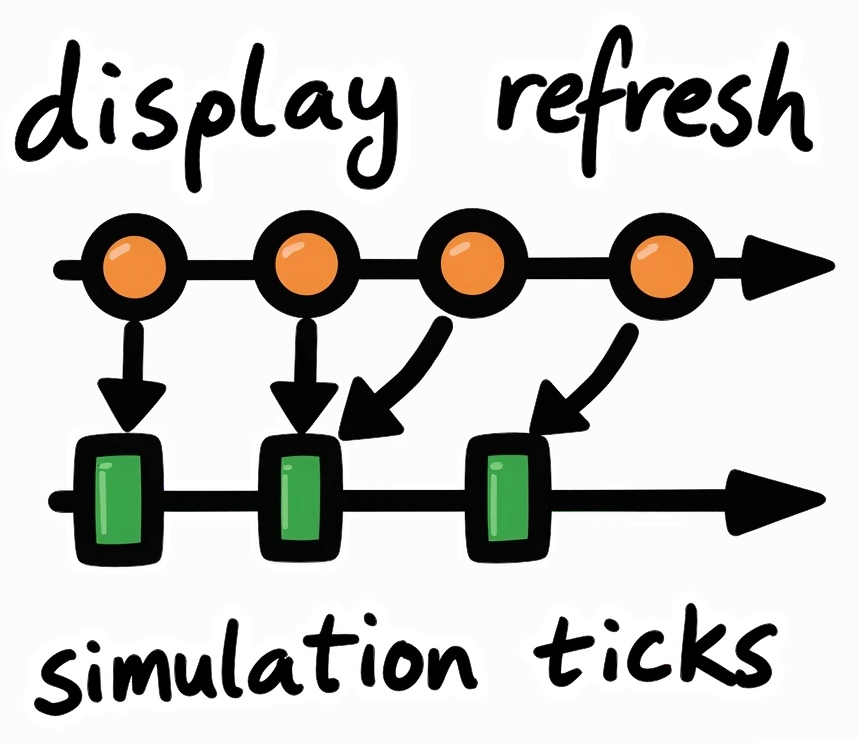
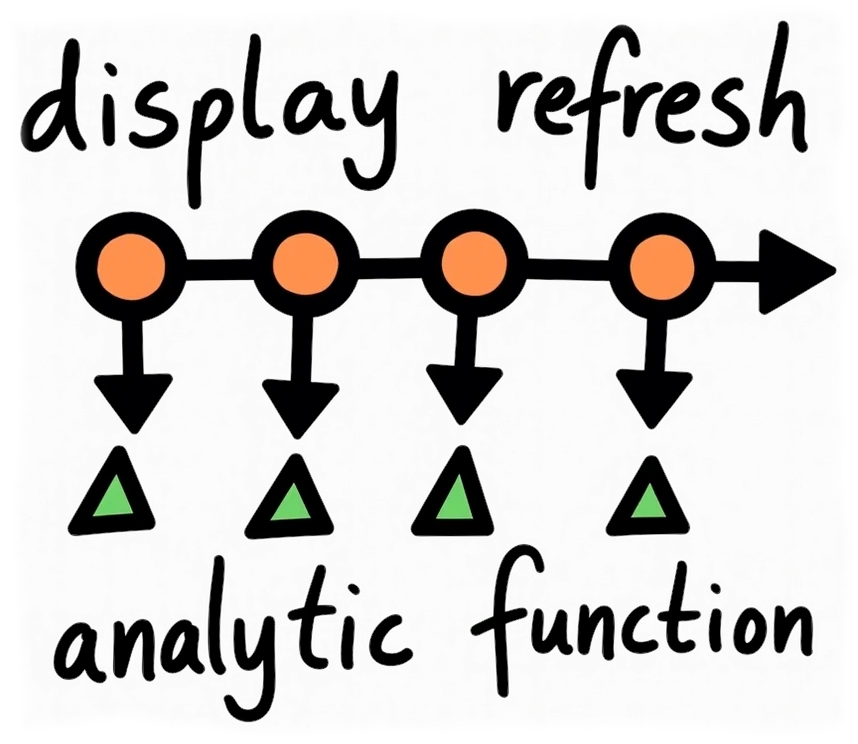Easy to integrate

No complex interactions

Analytic animation

Linear Approach

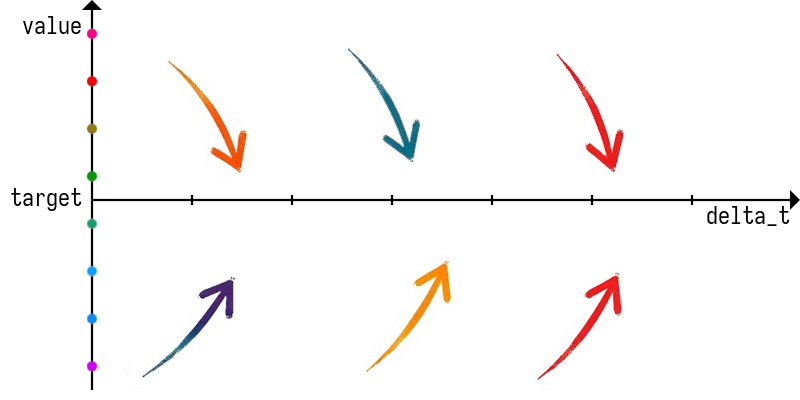
function LinearApproach(value, velocity, target, delta_t) {
  value -= target;
  value = Math.max(Math.abs(value) - delta_t * velocity, 0)
        * Math.sign(value);
  return value + target;
}

Exponential Approach

x = LERP(x, target, 0.1)

function ExponentialApproach(value, half_t, target, delta_t) {
  value -= target;
  value *= Math.pow(0.5, -delta_t / half_t);
  return value + target;
}

function ExponentialApproach(value, half_t, target, delta_t) {
  return value
       + (value - target) * Math.expm1(-delta_t / half_t * Math.LN2);
}

Animating periodic values

while (value < target - period/2) value += period;
while (value > target + period/2) value -= period;

value = std::remainder(value - target, range) + target;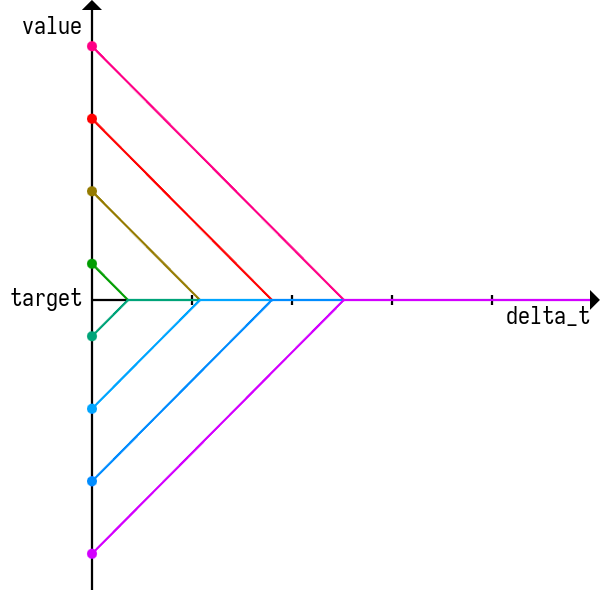

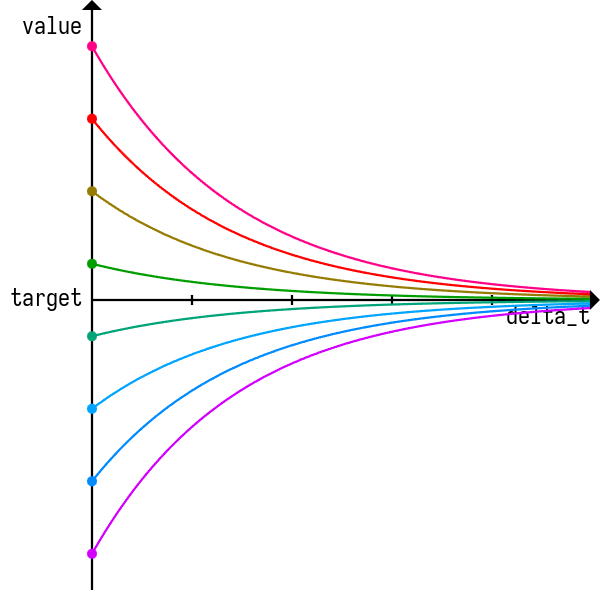
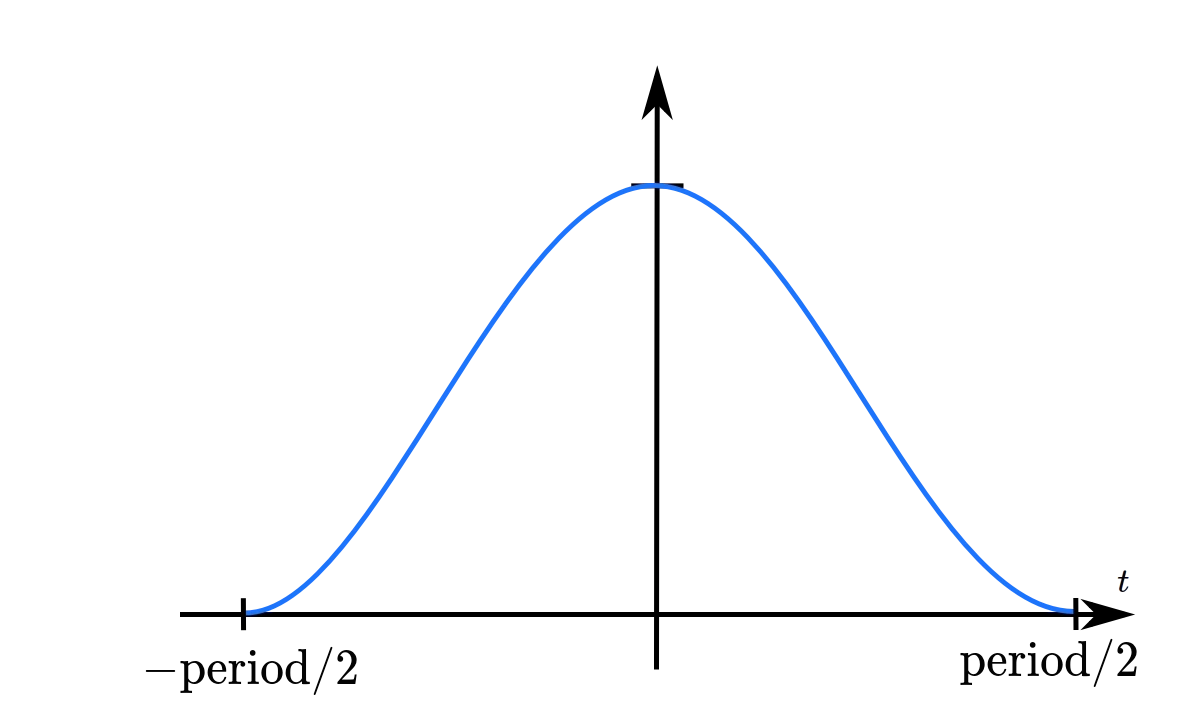
Maintaining Velocity

Sine Approach

Sine Approach

function SineApproach(value, velocity, period, target, delta_t) {
  let P1 = 2 * Math.PI / Number(period);
  let y = value - target;
  let v = velocity;

  let a; // a = amplitude / 2!
  if (Math.abs(velocity) < 1e-6) {
    a = y / 2;
  } else {
    a = (v * v / P1 / P1 + y * y) / y / 2;
  }

  if (Math.abs(a) > Math.abs(y)) a = y;

  if (v < -Math.abs(a) * P1) {
    v = -Math.abs(a) * P1;
  } else if (v > Math.abs(a) * P1) {
    v = Math.abs(a) * P1;
  }
  let fract = Math.abs((a * P1 + v) / (a * P1 - v));
  let x = -2 * Math.atan(Math.sqrt(fract));
  if (isNaN(x)) x = 0;
  
  if (x > Math.PI / 2) x -= Math.PI * 2;
  x += delta_t * P1;
  if (x > Math.PI / 2) x = Math.PI / 2;

  return [a * (1 - Math.sin(x)) + target, // new value
         -a * P1 * Math.cos(x)];          // new velocity
}

Spring Approach

Spring Approach

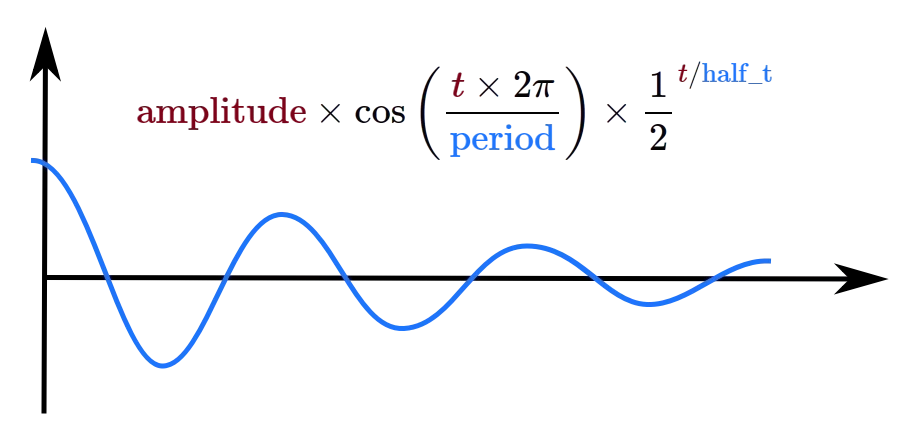
function SpringApproach(value, velocity, period, half_life, target, delta_t) {
  let P1 = 2 * Math.PI / period;
  let P2 = -1 / Math.LOG2E / half_life;
  let y = value - target; // y = a * cos(t * P1) * exp(t * P2)
  let v = velocity;       // v = a * exp(t * P2) * (P2 * cos(t * P1) - P1 * sin(t * P1))

  let arg = P1 * y / Math.sqrt(P1 * P1 * y * y + P2 * P2 * y * y - 2 * P2 * v * y + v * v);
  if (isNaN(arg)) {
    return [target, 0];
  }

  let ts = [-Math.acos(-arg) / P1, Math.acos(-arg) / P1, Math.acos(arg) / P1, -Math.acos(arg) / P1];

  let best_t, best_a;
  let best_t_err = Infinity;
  for (let t of ts) {
    let a = y / Math.cos(t * P1) / Math.exp(t * P2);
    let new_v = a * Math.exp(t * P2) * (P2 * Math.cos(P1 * t) - P1 * Math.sin(P1 * t));
    let err = Math.abs(velocity - new_v);
    if (err < best_t_err) {
      best_t = t;
      best_a = a;
      best_t_err = err;
    }
  }

  let t = best_t + delta_t;
  let a = best_a;
  return [a * Math.exp(t * P2) * Math.cos(t * P1) + target,                        // new value
          a * Math.exp(t * P2) * (P2 * Math.cos(P1 * t) - P1 * Math.sin(P1 * t))]; // new velocity
}

Let's look at moving objects

Warp Approach

function WarpApproach(value, velocity, warp_time, warp_dist, target, delta_t) {
  let y = (value - target) / warp_dist;
  let v = velocity * warp_time / warp_dist;
  let angle = Math.atan(v);

  let a_sign = y <= 0 ? 1 : -1;
  let a_x = Math.cos(angle + Math.PI / 2 * a_sign);
  let a_y = y + Math.sin(angle + Math.PI / 2 * a_sign);

  let b_x, b_y = -a_sign;
  if (a_x < 0 && Math.abs(b_y - y) <= 1 && Math.abs(y) < Math.abs(a_y + b_y) / 2) {
    b_x = Math.sqrt(1 - (b_y - y) * (b_y - y)); // B tangent to current position
  } else if (Math.abs(a_y) < 1) {               // B tangent to A
    b_x = a_x + Math.sqrt(4 - (b_y - a_y) * (b_y - a_y));
  } else {                                      // B on the right side of A
    b_x = a_x + 2;
  }

  let x = delta_t / warp_time, y_result, dir = 0;
  if (x >= b_x) {
    return [target, 0];
  } else if (x < (a_x + b_x) / 2) {
    let alpha = Math.acos(x - a_x);
    dir = 1 / Math.tan(alpha) * a_sign * warp_dist / warp_time;
    y_result = -a_sign * Math.sin(alpha) + a_y;
  } else {
    let alpha = Math.acos(x - b_x);
    dir = -1 / Math.tan(alpha) * a_sign * warp_dist / warp_time;
    y_result = a_sign * Math.sin(alpha) + b_y;
  }

  return [y_result * warp_dist + target, dir];
}

Approach comparison

Responsive Dragging

    function AnimationFrame(t) {
      ...
      [screenX, velocityX] = SpringApproach(screenX, velocityX, 0.4, 0.2, /* targetX */ mouseX, delta_t);
      [screenY, velocityY] = SpringApproach(screenY, velocityY, 0.4, 0.2, /* targetY */ mouseY, delta_t);
      ...
    }

    onmousemove = function(event) {
      ...
      screenX += event.movementX;
      screenY += event.movementY;
      ...
    }

Responsive Snapping

let Snap = function (x, y): [number, number] { ... }

    onmousemove = function(event) {
      ...
      [targetX, targetY] = Snap(event.clientX, event.clientY);
      if (targetX != lastX || targetY != lastY) {
        screenX += event.movementX;
        screenY += event.movementY;
      }
      [lastX, lastY] = [targetX, targetY];
      ...
    }

Reparenting Widgets

1. Find initial transform \(\mathbf{A}\)
2. Reparent widget
3. Find new transform \(\mathbf{B}\)
4. Offset the widget by \(-\mathbf{B} + \mathbf{A}\)
5. Animate offset \(\rightarrow 0\)

div.addEventListener('mouseenter', function (e) {
  let A = star.getBoundingClientRect();
  e.target.appendChild(star);
  let B = star.getBoundingClientRect();
  star.offsetX += A.left - B.left;
  star.offsetY += A.top - B.top;
});

Reparenting With Matricies

getComputedStyle(elem).transform

Avoiding Power Draw

var needsAnimationFrame;
var animating = false;
function Frame(t) {
  needsAnimationFrame = false;
  ...
  if (needsAnimationFrame) {
    requestAnimationFrame(Frame);
  } else {
    animating = false;
  }
}
function StartAnimation() {
  if (!animating) {
    requestAnimationFrame(Frame);
    animating = true;
  }
}

Tearing Can Be Awesome

End-to-end latency is lower for sound!

Thank you :)